Integration

Integration is quite simply the opposite of differentiating. Unfortunately actually integrating isn’t that easy or much fun at all!

The first and simplest way to integrate is:

\int{x^n}{dx} = \frac{x^{n+1}}{n+1}

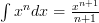
That basically means add 1 to the power of the ‘x‘ and then divide that by the new total value of the power. Like usual the easiest way to understand this is by seeing it.

\int{x^2}{dx} = \frac{x^3}{3} = \frac{1}{3} x^3

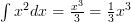
As with differentiation you can use any value of ‘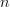n‘ and it’ll still work.

There are many different rules to integrating, and it’s best to try and remember them as they make integrating a lot easier!

Rule One

If you need to integrate a function that is mulitplied by a constant then you can move the constant outside of the integration formula, integrate the function then multiply it by the constant again.

\int{C*f(x)}{dx} = C\int{f(x)}{dx}

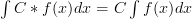
And here’s a quick example to help you get the gist of it:

\int{5\sin x}{dx} = 5\int{\sin x}{dx} = -5\cos x

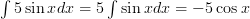
Rule Two

If you need to integrate two functions that are being added together, then you can seperate the functions, integrate them seperately and finally add them back together.

\int{f(x) \pm g(x)}{dx} = \int{f(x)}{dx} \pm \int{g(x)}{dx}

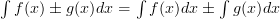
Here’s an example for your viewing pleasure!

\int{5x^2 + 4e^x}{dx} = \int{5x^2}{dx} + \int{4e^x}{dx}

= 5\int{x^2}{dx} + 4\int{e^x}{dx}

= 5(\frac{x^3}{3}) + 4(e^x) = \frac{5}{3}x^3 + 4e^x

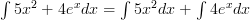
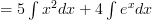
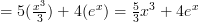
Rule Three

This ones a little bit harder to get your head around, but practise makes perfect! Basically you can add a constant to a function without affecting it, if ‘x‘ is in the first degree i.e. it has no power.

if 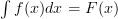\int{f(x)}{dx} = F(x)

then 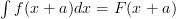\int{f(x+a)}{dx} = F(x+a)

Here’s how it looks with some actual numbers in:

\int{x^3}{dx} = \frac{x^4}{4}

\int{(x+5)^3}{dx} = \frac{(x+5)^4}{4}

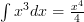
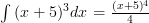
Rule Four

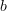This one works if ‘a‘ and ‘b‘ are constants and applied to a function of ‘x‘. To be honest the easiest way to understand it is by looking at this:

if 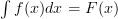\int{f(x)}{dx} = F(x)

then 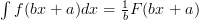\int{f(bx+a)}{dx} = \frac{1}{b} F(bx+a)

Still confused? I am a little bit, here’s one with numbers, see if that helps.

\int{x}{dx} = \frac{x^2}{2}

\int{3x+4}{dx} = \frac{1}{3} \frac{(3x+4)^2}{2} = \frac{(3x+4)^2}{6}

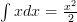
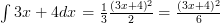
These rules come in very useful, and sometimes you’ll need to use a mixture of these rules with the methods of integration to find the final answer.

Leave a Reply