Differentiation

Definition: Differentiation is the act of finding the derivative of an equation. The derivative is a measure of how a function changes as it’s input changes.

Excercises.

The Power Rule

The first and most basic rule of differentiation is the power rule. Here is what it formally looks like:

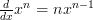
It looks horrible doesn’t it, but what it means is rather much simpler.

The left hand side (which will be abbreviated to LHS from now on) basically says “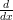” which means differentiate ““.

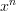The right hand side (which will be abbreviated to RHS) is quite simply the result.

To get to the answer we’ll start by looking at the LHS. We take the ‘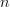‘ down from the ‘‘ and place it in front of the ‘‘ on the the other side:

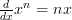
Then we minus 1 from ‘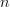‘ and place it as the power of the ‘‘:

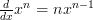
Which leaves us with the answer! Now it all seems very simple let’s try with a real example.

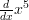
We start by taking the ‘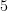‘ down and placing it in front of the ‘‘ on the other side:

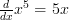
Then we minus 1 from the ‘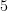‘ and place it as the power to the ‘‘ on the RHS and we have the answer:

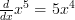
This method works for any value of ‘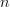‘. For example:

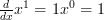
Even negative numbers:

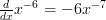
This allows us to find the derivatives of ‘‘: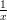

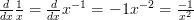
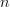‘‘ doesn’t even have to be a whole number! For example:

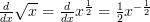
In fact ‘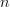‘ can be almost anything you want, even a symbol or ‘‘:

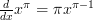
The Product Rule

The next rule you need to know is the product rule. It’s formal definition is this:

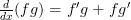
From the LHS of the equation we can tell that it is asking us to find the derivative of ‘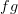‘. Unlike with the power rule, it’s asking us to differentiate two separate functions which are multiplied together; ‘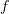‘ and ‘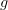‘. Unfortunately it isn’t as easy as just differentiating each function and adding them together.

The easiest way to explain what to do is with an example:

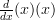
This, the LHS, shows us ‘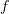‘ and ‘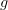‘, which for this example are very simple. Now we need to differentiate each part separately:

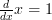and

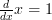
Then we multiply ‘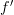‘ (which is the derivative of ‘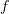‘ we just calculated) with the original ‘‘.

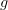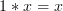
And vice versa, we multiply ‘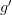‘ with the original ‘‘.

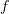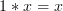
Then to get the final answer we simply add them together and we get:

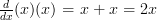
We know this is correct because we can test it using the power rule:

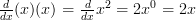
Now it’s been broken down it really isn’t as daunting as it once seemed! So let’s try a slightly more difficult example.

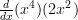
So first thing first, let’s differentiate both functions:

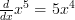and

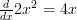
Then we multiply each derivative by the other original function:

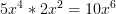and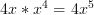

Finally add both of these together to get the final answer:

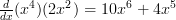
The Quotient Rule

The third rule that comes in very useful is the quotient rule. Once again the horrible formal definition:

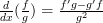
This is similar to the product rule to the extent it wants you to differentiate two functions, this time however the two functions are dividing each other.

Hopefully you’re getting the gist of it by now but we’ll go through an example anyway.

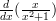
So we’ll start by finding the derivative of ‘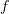‘ and ‘‘:

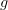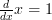and

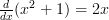
Then we just have to piece it all back together as the formal definition suggests:

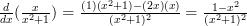
That one took a little bit longer, but it’s really not that difficult!

The Chain Rule

Now we have the first three rules down it’s time for the chain rule. The chain rule is used to find the derivative of a function of a function (if that makes sense!) and here is the formal definition:

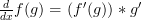
At first that looks quite daunting but it doesn’t require any new skills compared to the last three rules. Basically you take each function, differentiate it and sew them back together as the definition suggests. Once again the best way to learn how it works is by example.

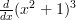
Here’s where the first big difference becomes apparent, as we can’t simply just take the two functions separately. What we need to do is replace ‘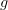‘ with another symbol, it’s typical to use ‘‘. Now I’ll show you what all the separate parts are:

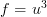and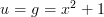

Now we can differentiate ‘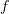‘ and ‘‘ the same ways we normally would:

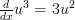and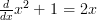

And now we just have to piece it all back together:

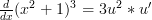
Substitute the ‘‘ for its value and you have the final answer:

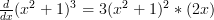
These rules can be used in combination with each other to break down and solve more complicated functions. There are only a few more rules to learn and you’ll be set for life!

How To Differentiate Trigonometric Functions

Differentiating trigonometric functions is fairly easy. The most important two thing to remember are:

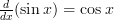
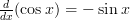
If you can remember these two facts then you can differentiate any function containing ‘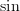‘ or ‘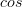‘, as they just end up looping round:

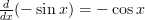
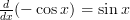
A short rhyme to remember this could be “Sine keeps it’s sign”, because whenever you differentiate ‘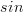‘ it keeps it sign, whether that be positive or negative. The opposite applies to ‘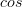‘, where if it starts off positive, once differentiated it’ll be negative.

At this point it’s probably worthwhile having a quick check at the trigonometry guide to brush up on your identities!